Analysis
Last modified: February 14, 2023
Contents
Contour
contour_bottom
FloatVector contour_bottom ()
| Operates on: | Image [OneBit] |
|---|---|
| Returns: | FloatVector |
| Category: | Analysis/Contour |
| Defined in: | contour.py |
| Author: | Michael Droettboom |
Returns a float vector containing the contour at the bottom of the image.
If there are no black pixels in a given column, the value is set to inf.
Example 1: contour_bottom()

result = array('d', [23.0, 24.0, 25.0, 26.0, 27.0, 44.0, 37.0, 33.0, 30.0, 28.0, 26.0, 25.0, 23.0, 22.0, 22.0, 21.0, 20.0, 8.0, 8.0, 7.0, 7.0, 6.0, 5.0, 5.0, 5.0, 4.0, 4.0, 4.0, 4.0, 3.0, 3.0, 3.0, 2.0, 2.0, 2.0, 2.0, 2.0, 2.0, 2.0, 2.0, 2.0, 2.0, 1.0, 2.0, 2.0, 2.0, 3.0, 3.0, 3.0, 3.0, 4.0, 4.0, 4.0, 5.0, 5.0, 5.0, 6.0, 7.0, 7.0, 67.0, 68.0, 68.0, 68.0, 69.0, 69.0, 71.0, 72.0, 74.0, 75.0, 77.0])
contour_left
FloatVector contour_left ()
| Operates on: | Image [OneBit] |
|---|---|
| Returns: | FloatVector |
| Category: | Analysis/Contour |
| Defined in: | contour.py |
| Author: | Michael Droettboom |
Returns a float vector containing the contour at the left of the image.
If there are no black pixels in a given row, the value is set to inf.
Example 1: contour_left()

result = array('d', [42.0, 40.0, 40.0, 50.0, 53.0, 55.0, 57.0, 58.0, 59.0, 60.0, 61.0, 61.0, 62.0, 62.0, 63.0, 64.0, 64.0, 63.0, 63.0, 65.0, 65.0, 65.0, 65.0, 65.0, 64.0, 64.0, 52.0, 50.0, 49.0, 48.0, 26.0, 23.0, 22.0, 19.0, 18.0, 17.0, 16.0, 15.0, 14.0, 13.0, 13.0, 12.0, 11.0, 10.0, 10.0, 9.0, 9.0, 8.0, 8.0, 7.0, 7.0, 7.0, 7.0, 6.0, 6.0, 4.0, 5.0, 6.0, 6.0, 6.0, 6.0, 6.0, 6.0, 6.0, 7.0, 7.0, 7.0, 7.0, 8.0, 8.0, 8.0, 9.0, 9.0, 3.0, 1.0, 0.0, 0.0, 0.0, 13.0, 15.0, 16.0, 17.0, 18.0, 20.0, 22.0, 24.0, 27.0, 34.0, inf, inf, inf, inf, 17.0, 19.0, 21.0, 22.0, 25.0, 29.0, 32.0, 42.0])
contour_pavlidis
[object] contour_pavlidis ()
| Operates on: | Image [OneBit] |
|---|---|
| Returns: | [object] |
| Category: | Analysis/Contour |
| Defined in: | contour.py |
| Author: | Andreas Leuschner |
Returns a point list of the outer contour trace found with Pavlidis' algorithm (T. Pavlidis: Algorithms for Grapics and Image Processing. pp. 129-165, Springer, 1982).
Note that this extracts only the first contour found, so this method should be applied to a single connected component. If you have an image with more than one connected component, do a CC analysis before, as in the following example:
ccs = img.cc_analysis()
contours = []
for cc in ccs:
contours.append([Point(p.x + cc.offset_x, p.y + cc.offset_y) \
for p in cc.contour_pavlidis()])
contour_right
FloatVector contour_right ()
| Operates on: | Image [OneBit] |
|---|---|
| Returns: | FloatVector |
| Category: | Analysis/Contour |
| Defined in: | contour.py |
| Author: | Michael Droettboom |
Returns a float vector containing the contour at the right of the image.
If there are no black pixels in a given row, the value is set to inf.
Example 1: contour_right()

result = array('d', [17.0, 14.0, 12.0, 11.0, 9.0, 8.0, 7.0, 6.0, 5.0, 4.0, 3.0, 3.0, 3.0, 2.0, 2.0, 1.0, 1.0, 1.0, 1.0, 1.0, 2.0, 1.0, 1.0, 1.0, 2.0, 2.0, 3.0, 4.0, 4.0, 5.0, 6.0, 6.0, 8.0, 11.0, 12.0, 14.0, 16.0, 18.0, 27.0, 27.0, 27.0, 16.0, 15.0, 15.0, 16.0, 27.0, 27.0, 27.0, 27.0, 27.0, 27.0, 27.0, 27.0, 27.0, 16.0, 16.0, 16.0, 16.0, 16.0, 16.0, 17.0, 17.0, 17.0, 17.0, 17.0, 27.0, 28.0, 28.0, 28.0, 28.0, 28.0, 29.0, 31.0, 33.0, 34.0, 17.0, 14.0, 15.0, 15.0, 16.0, 18.0, 19.0, 20.0, 22.0, 24.0, 26.0, 29.0, 33.0, inf, inf, inf, inf, 12.0, 12.0, 14.0, 15.0, 18.0, 21.0, 25.0, 28.0])
contour_samplepoints
[object] contour_samplepoints (int(1, 100) percentage = 25, Choice [outer_projection|full_contour] contour = outer_projection)
| Operates on: | Image [OneBit] |
|---|---|
| Returns: | [object] |
| Category: | Analysis/Contour |
| Defined in: | contour.py |
| Author: | Oliver Christen |
Returns a point vector containing contour points of the given image.
- percentage:
- return percentage of contour points. The points are selected approximately equidistant on the contour.
- contour:
- when 0 ("outer_projection"), the points returned by contour_left etc. are used; when 1 ("full_contour") the points returned by outline(1) are used.
In addition to the points determined by the percentage argument the result list also contains the four extreme points (topmost, leftmost, bottommost, rightmost).
ccs = image.cc_analysis()
points = []
for cc in ccs:
for samplepoint in cc.contour_samplepoints(50):
points.append(samplepoint)
Example 1: contour_samplepoints(10)

result = [Point(0, 75), Point(10, 43), Point(20, 33), Point(30, 30), Point(40, 1), Point(50, 0), Point(60, 4), Point(67, 11), Point(69, 23), Point(59, 33), Point(55, 43), Point(43, 53), Point(53, 63), Point(37, 73), Point(48, 83), Point(49, 97), Point(7, 67), Point(17, 92), Point(27, 96), Point(37, 98), Point(50, 96), Point(53, 4), Point(63, 14), Point(64, 24), Point(7, 50), Point(7, 64), Point(22, 84), Point(42, 0), Point(69, 15), Point(42, 99), Point(0, 77)]
contour_top
FloatVector contour_top ()
| Operates on: | Image [OneBit] |
|---|---|
| Returns: | FloatVector |
| Category: | Analysis/Contour |
| Defined in: | contour.py |
| Author: | Michael Droettboom |
Returns a float vector containing the contour at the top of the image.
If there are no black pixels in a given column, the value is set to inf.
Example 1: contour_top()

result = array('d', [75.0, 74.0, 74.0, 73.0, 55.0, 55.0, 53.0, 49.0, 47.0, 45.0, 43.0, 42.0, 41.0, 39.0, 38.0, 37.0, 36.0, 35.0, 34.0, 33.0, 33.0, 33.0, 32.0, 31.0, 31.0, 31.0, 30.0, 30.0, 30.0, 30.0, 30.0, 40.0, 39.0, 39.0, 38.0, 37.0, 36.0, 36.0, 35.0, 34.0, 1.0, 1.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 1.0, 1.0, 1.0, 2.0, 2.0, 3.0, 4.0, 4.0, 5.0, 6.0, 7.0, 8.0, 9.0, 10.0, 13.0, 15.0])
diagonal_projections
object diagonal_projections ()
| Operates on: | Image [OneBit] |
|---|---|
| Returns: | object |
| Category: | Analysis |
| Defined in: | projections.py |
| Author: | Michael Droettboom and Karl MacMillan |
Computes diagonal projections of an image by rotating it in 45 degrees, and then calculating the horizontal and vertical projections of the rotated image.
If the GUI is being used, the result is displayed in a window
histogram
FloatVector histogram ()
| Operates on: | Image [GreyScale|Grey16] |
|---|---|
| Returns: | FloatVector |
| Category: | Analysis |
| Defined in: | image_utilities.py |
| Author: | Michael Droettboom and Karl MacMillan |
Compute the histogram of the pixel values in the given image. Returns a Python array of doubles, with each value being a percentage.
If the GUI is being used, the histogram is displayed.
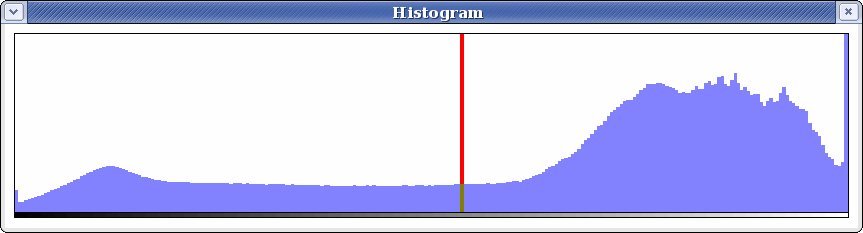
Example 1: histogram()
result = array('d', [0.0, 0.0, 0.00030321406913280777, 0.00015160703456640388, 0.0, 0.0, 0.0, 0.00015160703456640388, 0.00030321406913280777, 0.0, 0.00030321406913280777, 0.0, 0.00030321406913280777, 0.0, 0.00015160703456640388, 0.00030321406913280777, 0.00015160703456640388, 0.001212856276531231, 0.001212856276531231, 0.0007580351728320194, 0.0013644633110976349, 0.0007580351728320194, 0.001061249241964827, 0.001212856276531231, 0.0015160703456640388, 0.0006064281382656155, 0.0013644633110976349, 0.0016676773802304426, 0.0015160703456640388, 0.0013644633110976349, 0.001212856276531231, 0.0013644633110976349, 0.0009096422073984233, 0.0013644633110976349, 0.0006064281382656155, 0.0015160703456640388, 0.001212856276531231, 0.0018192844147968466, 0.001212856276531231, 0.00045482110369921165, 0.0013644633110976349, 0.00045482110369921165, 0.001061249241964827, 0.00030321406913280777, 0.00045482110369921165, 0.00015160703456640388, 0.00045482110369921165, 0.00045482110369921165, 0.00015160703456640388, 0.0, 0.00015160703456640388, 0.00045482110369921165, 0.0007580351728320194, 0.00030321406913280777, 0.0, 0.00045482110369921165, 0.0007580351728320194, 0.00045482110369921165, 0.00030321406913280777, 0.00030321406913280777, 0.00030321406913280777, 0.00030321406913280777, 0.00015160703456640388, 0.0006064281382656155, 0.00045482110369921165, 0.00015160703456640388, 0.00030321406913280777, 0.0007580351728320194, 0.001212856276531231, 0.00030321406913280777, 0.00045482110369921165, 0.00045482110369921165, 0.00045482110369921165, 0.0007580351728320194, 0.00030321406913280777, 0.00045482110369921165, 0.00030321406913280777, 0.0006064281382656155, 0.0009096422073984233, 0.001061249241964827, 0.0007580351728320194, 0.00030321406913280777, 0.00030321406913280777, 0.00030321406913280777, 0.00030321406913280777, 0.00015160703456640388, 0.001212856276531231, 0.00045482110369921165, 0.00045482110369921165, 0.0009096422073984233, 0.0007580351728320194, 0.00030321406913280777, 0.0016676773802304426, 0.001061249241964827, 0.00030321406913280777, 0.0006064281382656155, 0.0006064281382656155, 0.00045482110369921165, 0.0006064281382656155, 0.001061249241964827, 0.001212856276531231, 0.0006064281382656155, 0.0009096422073984233, 0.0013644633110976349, 0.0015160703456640388, 0.0015160703456640388, 0.001061249241964827, 0.0006064281382656155, 0.0006064281382656155, 0.0006064281382656155, 0.0007580351728320194, 0.0009096422073984233, 0.0007580351728320194, 0.001061249241964827, 0.0013644633110976349, 0.0013644633110976349, 0.001212856276531231, 0.001061249241964827, 0.0007580351728320194, 0.0016676773802304426, 0.001212856276531231, 0.00045482110369921165, 0.001061249241964827, 0.0013644633110976349, 0.001212856276531231, 0.002122498483929654, 0.001061249241964827, 0.0009096422073984233, 0.0018192844147968466, 0.0019708914493632504, 0.0009096422073984233, 0.0006064281382656155, 0.0016676773802304426, 0.0019708914493632504, 0.0018192844147968466, 0.0016676773802304426, 0.0016676773802304426, 0.0016676773802304426, 0.0019708914493632504, 0.001212856276531231, 0.0013644633110976349, 0.0013644633110976349, 0.0015160703456640388, 0.0013644633110976349, 0.001212856276531231, 0.001061249241964827, 0.0013644633110976349, 0.001061249241964827, 0.0013644633110976349, 0.0009096422073984233, 0.001061249241964827, 0.0009096422073984233, 0.0007580351728320194, 0.0006064281382656155, 0.0016676773802304426, 0.0018192844147968466, 0.0013644633110976349, 0.00045482110369921165, 0.001061249241964827, 0.0013644633110976349, 0.001061249241964827, 0.0013644633110976349, 0.001212856276531231, 0.0009096422073984233, 0.0009096422073984233, 0.001212856276531231, 0.0013644633110976349, 0.002122498483929654, 0.0019708914493632504, 0.001212856276531231, 0.001212856276531231, 0.002425712553062462, 0.0016676773802304426, 0.0018192844147968466, 0.0027289266221952697, 0.002880533656761674, 0.002425712553062462, 0.002425712553062462, 0.004548211036992117, 0.00469981807155852, 0.006215888417222559, 0.007731958762886598, 0.01015767131594906, 0.012583383869011523, 0.01607034566403881, 0.0156155245603396, 0.019254093389933294, 0.02107337780473014, 0.020921770770163734, 0.022589448150394178, 0.026682838083687082, 0.026834445118253485, 0.026682838083687082, 0.030321406913280776, 0.023347483323226198, 0.02653123104912068, 0.023347483323226198, 0.020163735597331717, 0.02274105518496058, 0.021224984839296544, 0.01834445118253487, 0.017738023044269254, 0.016221952698605217, 0.011067313523347484, 0.013341419041843541, 0.01015767131594906, 0.009854457246816252, 0.009702850212249849, 0.012431776834445117, 0.01015767131594906, 0.011825348696179502, 0.01015767131594906, 0.009854457246816252, 0.01137052759248029, 0.009854457246816252, 0.011522134627046696, 0.008944815039417828, 0.012431776834445117, 0.012583383869011523, 0.013947847180109158, 0.014705882352941176, 0.01364463311097635, 0.014251061249241965, 0.017889630078835657, 0.017738023044269254, 0.01804123711340206, 0.018950879320800484, 0.02001212856276531, 0.015463917525773196, 0.01212856276531231, 0.008035172832019405, 0.0036385688295936932, 0.0036385688295936932, 0.0027289266221952697, 0.0015160703456640388, 0.00030321406913280777, 0.00030321406913280777, 0.0007580351728320194, 0.00015160703456640388, 0.00015160703456640388, 0.00015160703456640388, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0])
min_max_location
object min_max_location (Image [OneBit] mask = None)
| Operates on: | Image [GreyScale|Grey16|Float] |
|---|---|
| Returns: | object |
| Category: | Analysis |
| Defined in: | image_utilities.py |
| Author: | Christoph Dalitz |
Returns the minimum and maximum pixel value and their location in an image. When the min/max value occurs at several locations, only the location that is closest to the bottom right corner is returned.
Only those pixels are examined that are black in the provided mask. When no mask is given, the entire image is examined. The mask can be useful, e.g., to find the lightest and darkest value in the original greyscale image belonging to a Cc, as in the following example:
onebit = grey.to_onebit() ccs = onebit.cc_analysis() # compute min/max of first cc in original greyscale image (pmin, vmin, pmax, vmax) = grey.min_max_location(ccs[0])
The return value is a tuple of the form (pmin, vmin, pmax, vmax) where pmin and pmax are the point of the minimum and maximum, respectively, and vmin and vmax the corresponding pixel values.
Example 1: min_max_location()
result = (Point(87, 49), 2, Point(83, 30), 240)
projection_cols
IntVector projection_cols ()
| Operates on: | Image [OneBit] |
|---|---|
| Returns: | IntVector |
| Category: | Analysis |
| Defined in: | projections.py |
| Author: | Michael Droettboom and Karl MacMillan |
Compute the vertical projections of an image. This computes the number of pixels in each column.
Example 1: projection_cols()

result = array('i', [3, 3, 2, 2, 2, 2, 11, 19, 24, 28, 32, 34, 37, 40, 41, 33, 28, 25, 24, 22, 20, 18, 17, 16, 15, 16, 18, 16, 16, 17, 17, 15, 15, 14, 16, 46, 48, 47, 46, 47, 48, 49, 51, 46, 14, 14, 17, 17, 18, 20, 22, 22, 23, 31, 26, 16, 11, 10, 11, 9, 9, 12, 14, 16, 20, 22, 20, 17, 13, 8])
projection_rows
IntVector projection_rows ()
| Operates on: | Image [OneBit] |
|---|---|
| Returns: | IntVector |
| Category: | Analysis |
| Defined in: | projections.py |
| Author: | Michael Droettboom and Karl MacMillan |
Compute the horizontal projections of an image. This computes the number of pixels in each row.
Example 1: projection_rows()

result = array('i', [12, 17, 19, 10, 9, 8, 7, 7, 7, 7, 7, 7, 6, 7, 6, 6, 6, 7, 7, 5, 4, 5, 5, 5, 5, 5, 6, 8, 9, 9, 17, 23, 25, 27, 25, 24, 24, 20, 18, 20, 20, 22, 22, 25, 21, 20, 15, 16, 17, 18, 17, 17, 16, 18, 19, 22, 21, 20, 20, 20, 20, 20, 20, 21, 20, 19, 18, 19, 19, 19, 19, 18, 16, 16, 18, 19, 24, 23, 24, 23, 27, 35, 33, 29, 25, 21, 15, 4, 0, 0, 0, 0, 6, 9, 11, 13, 22, 21, 14, 1])
projection_skewed_cols
object projection_skewed_cols (FloatVector Rotation angles)
| Operates on: | Image [OneBit] |
|---|---|
| Returns: | object |
| Category: | Analysis |
| Defined in: | projections.py |
| Author: | Christoph Dalitz |
Computes all vertical projections of an image skewed by a list of angles. As in rotate, angles are measured clockwise and in degrees. Thus a rotate followed by a projection_cols would be conceptually the same, albeit considerably slower.
This function is overloaded to work both with a single angle and a list of angles as input. In the first case a single projection vector is returned, in the second a list of projections vectors. This is explained in the following example:
# called twice with a single angle as input
proj1 = img.projection_skewed_cols(0.5)
proj2 = img.projection_skewed_cols(1.0)
# the same result with one function call
projlist = img.projection_skewed_cols([0.5,1.0])
proj1 = projlist[0]
proj2 = projlist[1]
Note that unlike rotate the image size is not extended. Image regions moved outside the original image size are simply clipped, which restricts this method to small angles.
Example 1: projection_skewed_cols(15.0)

result = array('i', [0, 26, 23, 20, 19, 18, 18, 21, 19, 20, 18, 18, 15, 19, 18, 19, 23, 26, 28, 29, 32, 38, 37, 41, 36, 38, 33, 29, 28, 24, 20, 16, 15, 6, 3, 9, 10, 12, 13, 12, 13, 18, 16, 13, 9, 6, 5, 7, 7, 6, 8, 9, 9, 9, 13, 12, 17, 22, 23, 23, 17, 16, 10, 2, 0, 0, 0, 0, 0, 0])
projection_skewed_rows
object projection_skewed_rows (FloatVector Rotation angles)
| Operates on: | Image [OneBit] |
|---|---|
| Returns: | object |
| Category: | Analysis |
| Defined in: | projections.py |
| Author: | Christoph Dalitz |
Computes all horizontal projections of an image skewed by a list of angles. For more details and an example see projection_skewed_cols.
Note that unlike rotate the image size is not extended. Image regions moved outside the original image size are simply clipped, which restricts this method to small angles.
Example 1: projection_skewed_rows(15.0)

result = array('i', [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 4, 9, 12, 9, 8, 7, 6, 7, 6, 5, 6, 6, 6, 6, 5, 7, 6, 6, 6, 6, 5, 6, 7, 8, 5, 12, 16, 19, 19, 23, 22, 26, 30, 33, 34, 42, 41, 37, 31, 23, 18, 17, 18, 21, 23, 22, 19, 18, 17, 19, 19, 20, 19, 19, 19, 20, 21, 21, 22, 23, 23, 25, 23, 22, 18, 19, 19, 18, 19, 14, 17, 17, 17, 12, 13, 12, 18, 26, 32, 30, 25, 18, 16, 5, 3, 3, 4, 5, 3])
projections
object projections ()
| Operates on: | Image [OneBit] |
|---|---|
| Returns: | object |
| Category: | Analysis |
| Defined in: | projections.py |
| Author: | Michael Droettboom and Karl MacMillan |
Computes the projections in both the row- and column- directions. This is returned as a tuple (rows, columns), where each element is an IntVector of projections. (Equivalent to (image.projections_rows(), image.projections_cols())).
If the GUI is being used, the result is displayed in a window:
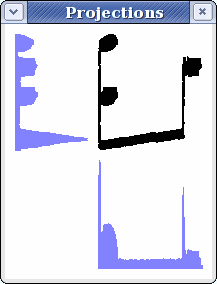
rotation_angle_projections
FloatVector rotation_angle_projections (float minangle = -2.50, float maxangle = 2.50, float accuracy = 0.00)
| Operates on: | Image [OneBit] |
|---|---|
| Returns: | FloatVector |
| Category: | Analysis |
| Defined in: | projections.py |
| Author: | Christoph Dalitz |
Estimates the rotation angle of a document with the aid of skewed projections, as described in section 3.1 of C. Dalitz, G.K. Michalakis, C. Pranzas: 'Optical Recognition of Psaltic Byzantine Chant Notation.' International Journal of Document Analysis and Recognition 11, pp. 143-158 (2008).
This method works for a wide range of documents (text, music, forms), but can become slow for large images. This particular implementation can be accelerated by reducing the number of black pixels in the image, eg. by scaling it down, only considering a fraction of the image or by removing 'uninteresting' pixels.
Arguments:
- minangle, maxangle (optional):
- angle interval that is searched for the skew angle; default values are -2.5 and +2.5
- accuracy (optional):
- error bound for the skew angle estimate; default value is zero
When accuracy is set to zero, a default value of 180*0.5/(image.ncols*pi) is used, which is only a heuristic formula for little changes in the projection profile.
Return Values:
- rotation angle:
- The rotation angle necessary to deskew the image. Can be used directly as input to rotate
- accuracy:
- Accuracy of the returned angle.