Gamera graph library

Last modified: February 14, 2023

Contents

Introduction
Using the graph library from Python
Reference
Implementation details
Using the Graph library from C++

Introduction

Gamera provides a rudimentary framework for dealing with graph structures. This library can be used from Python and from C++.

This chapter assumes a basic understanding of graph theory and graph algorithms. While this document describes the API, it does not describe in detail how the algorithms work. (Hopefully this can be added in a future release of this documentation.)

Using the graph library from Python

Most operations on graphs in the Gamera graph library are methods on Graph objects.

Each node is identified by an arbitrary Python value. Importantly, the same value may not be assigned to more than one node within the same graph. Whenever a node is needed as an argument, either the node object or the node's value may be passed in. In most cases, it is more convenient to refer to nodes by their associated values rather than keeping track of their associated Node objects.

The following example code covers basic usage. For more detailed descriptions of the properties and methods, see the Reference section.

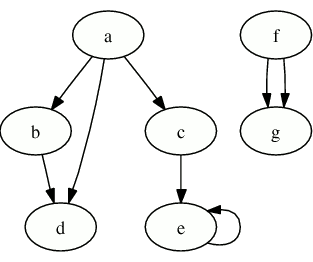
Let's look at some simple code to create the following trivially small graph structure:

>>> from gamera import graph
>>> from gamera import graph_util
>>>
>>> g = graph.Graph()
>>>
>>> g.add_edge('a', 'b')
1
>>> g.add_edge('a', 'c')
1
>>> g.add_edge('a', 'd')
1
>>> g.add_edge('b', 'd')
1
>>> g.add_edge('c', 'e')
1
>>> g.add_edge('f', 'g')
1
>>> g.add_edge('f', 'g')
1
>>> g.add_edge('e', 'e')
1
>>>

add_edge creates nodes that don't already exist, so add_node is not necessary to create this graph.

The number of nodes and edges can be queried:

>>> g.nnodes # Number of nodes
7
>>> g.nedges # Number of edges
8

Now, the graph can be traversed, using either a breadth-first search (BFS) or depth-first search (DFS). Each search algorithm takes a node as a starting point:

>>> # node is a Node instance.  Call node() to get its value
>>> for node in g.BFS('a'):
...    print node(),
...
a b c d e
>>> for node in g.DFS('a'):
...    print node(),
...
a d c e b
>>> # No other nodes reachable from 'e'
>>> for node in g.BFS('e'):
...    print node(),
...
e
>>> for node in g.BFS('f'):
...    print node(),
...
f g

Note that the search algorithms, like many other things in the Gamera graph library, return lazy iterators, so the results are determined on demand. Importantly, this means you cannot get the length of the result until it has been entirely evaluated.

>>> g.BFS('a')
<gamera.graph.Iterator object at 0xf6fa54d0>
>>> len(g.BFS('a'))
Traceback (most recent call last):
  File "<stdin>", line 1, in ?
TypeError: len() of unsized object
>>> list(g.BFS('a'))
[<Node of 'a'>, <Node of 'b'>, <Node of 'c'>, <Node of 'd'>, <Node of 'e'>]
>>> [node() for node in g.BFS('a')]
['a', 'b', 'c', 'd', 'e']
>>>

Note that this graph is composed of two distinct subgraphs. There are ways to determine the number of subgraphs and iterate over the roots of those subgraphs if the graph is undirected. For instance, to do a breadth-first search of all subgraphs:

>>> g.make_undirected()
>>> g.nsubgraphs
2
>>> for root in g.get_subgraph_roots():
...    for node in g.BFS(root):
...       print node.data,
...    print
...
a b c d e
f g

The graph can be restricted based on a number of different properties by passing flags to the constructor. These properties include directedness, cyclicalness, multi-connectedness and self-connectedness. (See Graph constructor).

For instance, let's attempt to make a tree, which is a graph that is undirected and contains no cycles, using the same graph structure:

>>> g = graph.Graph(graph.TREE | graph.CHECK_ON_INSERT)
>>> g.add_edge('a', 'b')
1
>>> g.add_edge('a', 'c')
1
>>> g.add_edge('a', 'd')
1
>>> g.add_edge('b', 'd')
0
>>> g.add_edge('c', 'e')
1
>>> g.add_edge('f', 'g')
1
>>> g.add_edge('f', 'g')
0
>>> g.add_edge('e', 'e')
0

Note that some edges were not created, since they would have violated the restrictions of a tree. This is indicated by the return value of add_edge. In this case, our graph now looks like this:

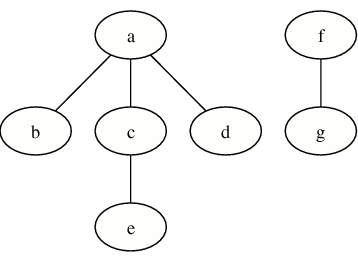
The reference section below provides a complete list of the algorithms and methods on graph objects.

Reference

`Graph` objects

Each graph is represented by instances of the Graph class. All modifications to the graph structure, including adding and removing nodes and edges, is performed through this class.

Basic methods

`Graph` Constructor

`Graph`

Graph (flags = FREE)

Construct a new graph.

The flags are used to set certain restrictions on the graph. When adding an edge violates one of these restrictions, the edge is not added and None is returned. Note that exceptions are not raised. The graph type may be changed at any time after creation using methods such as make_directed or make_undirected, but conversion may take some time.

The flags may be any combination of the following values (use bitwise-or to combine flags). The values of these flags are defined in the graph module. By default, all flags except of CHECK_ON_INSERT are True:

DIRECTED:

When True, the graph will have directed edges. Nodes will only traverse to other nodes in the direction of the edge.

CYCLIC:

When True, the graph may contain cycles. When False, edges are added to the graph only when they do not create cycles. (When False, MULTI_CONNECTED and SELF_CONNECTED are set to False.)

BLOB:

A "blob" is defined as the opposite of a tree. (When False, DIRECTED and CYCLIC will be set to False).

MULTI_CONNECTED:

When True, the graph may contain multiple edges between a single pair of nodes.

SELF_CONNECTED:

When True, the graph may contain edges that start and end at the same node.

CHECK_ON_INSERT:

When True, an edge is only inserted when it conforms all restrictions. This is disabled by default because the checks slow down adding edges significantly.

In addition to these raw flags, there are some convenience values for common combinations of these flags.

FREE: Equivalent to all flags being set. There are no restrictions on the graph morphology.

TREE: Tree structure (no flags set).

FLAG_DAG: Directed, acyclic graph.

UNDIRECTED: Undirected, cyclic graph.

Methods for Nodes

`add_node`

add_node (value)

Add a node identified by the given value. The newly-created node has no edges.

Returns 1 if a new node was created. Returns 0 if a node already exists with the associated value.

Complexity: Nodes are added in logarithmic time.

`add_nodes`

add_nodes (list_of_values)

Add nodes identified by each value in a list. The newly-created nodes have no edges.

Returns the number of new nodes that were created.

Complexity: add_nodes is moderately faster than multiple calls to add_node. Nodes are added in logarithmic time

`get_node`

get_node (value)

Returns the Node object identified by the given value.

Raises a ValueError exception if there is no node associated with the given value.

Complexity: Searching for a node takes O ( ln n ) time where n is the number of nodes in the graph.

`get_nodes`

get_nodes ()

Returns a lazy iterator over all nodes in the graph. The ordering of the nodes is undefined.

`has_node`

has_node (value)

Returns True if graph has a node identified by value.

Comlexity: Searching for an node takes O ( ln n ) time where n is the number of nodes in the graph.

`remove_node`

remove_node (value)

Remove a node identified by value from the graph, stitching together the broken edges.

For instance, given the graph:

a -> b -> c

.remove_node('b') will result in:

a -> c

Complexity: Removing a node takes O (n + e) where n is the number of nodes in the graph and e is the number of edges attached to the given node.

`remove_node_and_edges`

remove_node_and_edges (value)

Remove the node identifed by value from the graph, and remove all edges pointing inward or outward from that node.

For instance, given the graph:

a -> b -> c

.remove_node_and_edges('b') will result in:

a         c

Complexity: Removing a node takes O (n + e) where n is the number of nodes in the graph and e is the number of edges attached to the given node.

Methods for Edges

`add_edge`

add_edge (from_value, to_value, cost = 1.0, label = None)

Add an edge between the two nodes identified by from_value and to_value.

The return value is the number of edges created. If the graph has set the flag CHECK_ON_INSERT and the edge violates any of the restrictions specified the edge by the flags to the graph's constructor will not be created. If the graph is DIRECTED, the edge goes from from_value to to_value. If a node representing one of the values is not present, a node wille be implicitly created.

Optionally, a cost and label can be associated with the edge. These values are used by some higher-level graph algorithms such as create_minimum_spanning_tree or shortest_path.

Complexity: Edges are added in O ( ln n ) because of getting the nodes which are associated to from_value or to_value.

`add_edges`

add_edges (list_of_tuples)

Add edges specified by a list of tuples of the form:

(from_value, to_value, [cost*[, *label]]).

The members of this tuple correspond to the arguments to add_edge.

The return value is the number of edges created. For more information on adding edges see add_edge If an edge violates any of the restrictions specified

Complexity: add_edges is moderately faster than multiple calls to add_edge.

`get_edges`

get_edges ()

Returns an iterator over all edges in the graph. The ordering of the edges is undefined.

`has_edge`

has_edge (from_value, to_value)

or

has_edge (from_node, to_node)

or

has_edge (edge)

Returns True if graph contains the given edge. The edge can be specified as either a pair of values identifying nodes, a pair of Node objects, or a single Edge object.

Complexity: Searching for an edge takes O ( e + ln n ) time where e is the number of edges in the graph and n is the number of nodes in the graph.

`remove_edge`

remove_edge (from_value, to_value)

Remove an edge between two nodes identified by from_value and to_value.

If the edge does not exist in the graph, a RuntimeError exception is raised.

When the graph is DIRECTED, only the edge going from from_value to to_value is removed.

If the graph is MULTI_CONNECTED, all edges from from_value to to_value are removed.

Complexity: Edges can be removed in O*(*e) time where e is the number of edges in the graph.

`remove_all_edges`

remove_all_edges ()

Remove all the edges in the graph, leaving all nodes as islands.

Complexity: remove_all_edges takes O ( n + e) time where n is the number of nodes in the graph and e is the number of edges in the graph.

Directedness

`is_directed`

is_directed ()

Return True if the graph is defined as directed.

`is_undirected`

is_undirected ()

Return True if the graph is defined as undirected.

`make_directed`

make_directed ()

If the graph is undirected, converts it into an directed graph by adding a complementary edge for each existing edge. Complexity: The graph can be converted in O ( e ) time.

`make_undirected`

make_undirected ()

If the graph is directed, converts it into an undirected graph. Each edge in the existing graph will become a non-directional edge in the resulting graph.

Cyclicalness

`is_cyclic`

is_cyclic ()

Returns True if the graph has any cycles. Note that this is independent from the flag CYCLIC.

`is_acyclic`

is_acyclic ()

Returns True if the graph does not have any cycles.

`make_cyclic`

make_cyclic ()

Allow the graph to include cycles from this point on. This does nothing except set the CYCLIC flag.

`make_acyclic`

make_acyclic ()

Remove any cycles (using a depth-first search technique) and disallow cycles from this point on.

This may not be the most appropriate cycle-removing technique for all applications.

See create_spanning_tree for other ways to do this.

Blob vs. Tree

`is_tree`

is_tree ()

Returns True if the graph conforms to the restrictions of a tree.

`is_blob`

is_blob ()

Returns True if the graph does not conform to the restricitions of a tree.

`make_tree`

make_tree ()

Turns the graph into a tree by calling make_acyclic followed by make_undirected. Sets the BLOB flag to False.

This approach may not be reasonable for all applications. For other ways to convert blobs to trees, see spanning trees.

`make_blob`

make_blob ()

Make the graph into a blob (the opposite of a tree). This does nothing except set the BLOB flag.

Multi-connectedness

`is_multi_connected`

is_multi_connected ()

Returns True if the graph is multi-connected (multiple edges between a single pair of nodes).

`is_singly_connected`

is_singly_connected ()

Returns True if the graph does not have multiple edges between a single pair of nodes.

`make_multi_connected`

make_multi_connected ()

Allow the graph to be multi-connected from this point on. This does nothing except set the MULTI_CONNECTED flag.

`make_singly_connected`

make_singly_connected ()

For each pair of nodes, leave only one remaining edge in either direction. Restrict the graph to being singly-connected from this point on.

Self-connectedness

`is_self_connected`

is_self_connected ()

Returns True if the graph is self-connected. When True the graph has edges pointfrom from one node to that same node.

`make_self_connected`

make_self_connected ()

Allow the graph to be self-conncted from this point on. This does nothing except set the SELF_CONNECTED flag.

`make_not_self_connected`

make_not_self_connected ()

Remove all self-connections and restrict the graph to have no self-connections from this point on.

Subgraphs

Here, a "subgraph" is defined as a connected group of nodes. A graph contains multiple subgraphs when the graph does not have a single root node from which all other nodes can be reached.

`get_subgraph_roots`

get_subgraph_roots ()

Returns a lazy iterator over each of the subgraph roots. Performing a breadth-first or depth-first search from each of this nodes will visit every node in the graph. Currently this algorithm has been tested for undirected graphs only, but it should also work for directed graphs.

`size_of_subgraph`

size_of_subgraph (value)

or

size_of_subgraph (node)

Returns the size of the subgraph rooted at the given node. In other words, this returns the number of nodes reachable from the given node.

`is_fully_connected`

is_fully_connected ()

Returns True if there is only one subgraph in the graph. In other words it returns True if the number of nodes reachable from the first inserted node is equal to the overall number of nodes. Currently this algorithm is only defined for undirected graphs.

Utility

`copy`

copy (flags = FREE)

Copies a graph (optionally specifying new flags for the new graph).

In some cases, copying the graph to a new graph type may be faster than using one of the in-place conversion functions.

See Graph constructor for a definition of flags.

`has_flag`

has_flag (flag)

Returns True when the given flag is set in the graph. flag can be a single flag or or-combination of flags which are documented in Graph constructor .

`has_path`

has_path (from_node, to_node)

Returns True when to_node is reachable starting at start_node. start_node and to_node can be a Node object or a node's value.

Properties

nnodes:

The number of nodes in the graph.
nedges:

The number of edges in the graph.
nsubgraphs:

The number of subgraphs.

High-level algorithms

Search

`BFS`

BFS (value or node)

A lazy iterator that returns the nodes in breadth-first order starting from the given value or node. Note that the starting node is included in the returned nodes.

`DFS`

DFS (value or node)

A lazy iterator that returns the nodes in depth-first order starting from the given value or node. Note that the starting node is included in the returned nodes.

Shortest path

`dijkstra_shortest_path`

dijkstra_shortest_path (value or node)

Calculates the shortest path from the given node to all other reachable nodes using Djikstra's algorithm.

The return value is a dictionary of paths. The keys are destination node identifiers and the values are tuples of the form

(distance, nodes)

where distance is the distance traveled from the given node to the destination node and nodes is a list of node identifiers in the shortest path to reach the destination node.

This algorithm will use the cost values associated with each edge if they are given.

`shortest_path`

shortest_path (value or node)

An alias for dijkstra_shortest_path.

`dijkstra_all_pairs_shortest_path`

dijkstra_all_pairs_shortest_path ()

Calculates the shortest paths between all pairs of nodes in the graph by calling dijkstra_shortest_path multiple times.

The return value is a dictionary where the keys are source node identifiers and the values are dictionaries of paths keyed by destination node identifiers (of the same form as dijkstra_shortest_path). The values of the internal dictionaries are tuples of the form

(distance, nodes)

where distance is the distance traveled from the given node to the destination node and nodes is a list of node identifiers in the shortest path to reach the destination node.

This algorithm will use the cost values associated with each edge if they are given.

`all_pairs_shortest_path`

all_pairs_shortest_path ()

An alias for dijkstra_all_pairs_shortest_path.

Spanning trees

`create_spanning_tree`

create_spanning_tree (value or node)

Returns a new graph which is a (probably non-optimal) spanning tree of all nodes reachable from the given node. This tree is created using DFS.

`create_minimum_spanning_tree`

create_minimum_spanning_tree ()

Creates a minimum spanning tree of the entire graph in place using Kruskal's algorithm. A minimum spanning tree connects all nodes using the minimum total edge cost.

Partitions

`optimize_partitions`

optimize_partitions (root_node, fittness_func, max_parts_per_group = 5, max_subgraph_size = 16, criterion = "min")

A partition is defined as a way to divide a subgraph into groups. This algorithm finds an optimal partition according to the given fitness function.

root_node

The root node of the subgraph to be optimized.

fitness_func

A user-provided Python function, that given a partition as a nested list of groups, where each value is a node identifier, returns a floating-point score. Higher values indicate greater fitness.

max_parts_per_group

Limits the number of nodes that will be placed into a single group.

max_subgraph_size

If the subgraph rooted at root_node has more than max_subgraph_size nodes, the partitions will not be optimized

criterion

Choses the solution with the highest minimum ('min') or highest average ('avg') confidence.

Coloration

`colorize`

colorize (ncolors)

This method colors the graph using ncolors colors with the constraint that adjacent nodes have different colors. When the number of colors is too small for the given graph, a runtime_error is raised. The graph coloring algorithm is based on the "6-COLOR" alorithm for planar graphs, as described in:

D. Matula, Y. Shiloach, R. Tarjan: Two linear-time algorithms for five-coloring a planar graph. Tech Rep STAN-CS-80-830, Computer Science Dep., Stanford Univ., 1980

We have modified the algorithm in such a way that the color distribution is balanced, i.e. that each color is assigned approximately to the same number of nodes (also known as "equitable coloring").

Note

The coloring algorithm works in linear time and is only guaranteed to work for planar graphs and ncolors > 5. When the algorithm runs out of colors (e.g., because the graph is not planar), an exception is thrown.

`get_color`

get_color (value or node)

Returns the color of the node after the graph was colorized with colorize.

Node objects

Nodes contain a reference to an arbitrary Python value. Importantly, the value is used to identify the node, so the same value may not be assigned to more than one node. In many cases, it is much more convenient to refer to nodes by their associated values rather than keeping track of their associated Node objects.

Properties

data:

The value that identifies this node. (This value can also be obtained by "calling" the node as in node()).
edges:

A lazy iterator over the edges pointing out from the node.
nodes:

A lazy iterator over the nodes that can be reached directly (through a single edge) from this node.
nedges:

The number of edges going out from this node.

Edge objects

Methods

traverse

traverse (node)

Returns the node on the other end of the edge. (Useful only for undirected graphs).

Properties

from_node:

The starting node of this edge.
to_node:

The ending node of this edge.
cost:

The cost associated with traversing this edge (used by algorithms such as create_minimum_spanning_tree).
label:

The label associated with this edge.

Utilities

The following functions are available in the graph_util module.

`graphviz_output`

graphviz_output (graph, filename, string_function = str)

Writes a graph in the format used by the dot tool in the graphviz package for graph visualisation.

graph: A Gamera Graph object.
filename: Filename to output to.
string_function: A function to convert node values to strings. By default this will use Python's standard str function.

Implementation details

There are many ways to represent graphs in memory for different applications. Unfortunately, this library only uses one, which may not be suitable for all applications. It is as follows:

The graph object contains lists of all nodes and edges. Deleting nodes and edges is in linear time.

The graph contains a hash table from node data to nodes, so given a particular piece of data associated with a node, the node can be looked up in O(ln n) time.

Each node contains an array of coincident edges. If the graph is directed, this includes edges going in and out from the node.

Using the Graph library from C++

The module gamera.graph is only a thin Python wrapper around a C++ class Graph. This can also be used directly in C++ plugins.

Compilation and linkage

The header file graph.hpp declares the necessary structures in the namespace Gamera::Graph. It is installed with the other gamera header files, and can thus be included with

#include "graph/graph.hpp"
using namespace Gamera::Graph;

The tricky part is getting your plugin module to be linked with the actual graph implementation. This is achieved by adding the source files to the cpp_sources property in the plugin Python interface.

In the gamera core code, the following works:

class ExampleModule(PluginModule):
    category = "MyPlugins"
    cpp_headers = ["myplugins.hpp"]
    import glob
    cpp_sources = glob.glob("src/graph/*.cpp")
    functions = [myplugin1, myplugin2]
module = ExampleModule()

In a toolkit, this will not work, because the path names in the cpp_sources property are relative to the location of the setup.py script. To allow for the use of the Graph C++ class in toolkits, the source files are installed together with Gamera. You can thus specify this file in cpp_sources as follows:

class ExampleModule(PluginModule):
    # ...
    import os, gamera
    gamera_root = os.path.dirname(gamera.__file__)
    import glob
    cpp_sources = (glob.glob(os.path.join(gamera_root, "gamera/src/graph/*.cpp")))
    # ...

Usage

Most methods are similar to them in the Python wrapper. For a detailed description you can see more details in the implementation and header files of Graph. A node is designed for storing a class derived from GraphData. Be sure storing your GraphData objects as long as your Graph lives. GraphData defines the virtual methods which must be implemented in your derived class.

virtual GraphData* copy ()

copies a given Data element. Note that this will not be deleted automatically.

virtual int compare (const GraphData& b)

returns 0 if b and *this are equal

returns <0 if *this < b

returns >0 if *this > b

The comparison operators < > == != <= >= are mapped to this method.

You can see some examples for derived classes in graphdataderived.hpp

Example

Here is a very short example for a C++-Usage:

#include "graph/graph.hpp"

void test() {
   Graph* g = new Graph(FLAG_UNDIRECTED);
   GraphDataUnsignedInt* data1 = new GraphDataUnsignedInt(42);
   GraphDataUnsignedInt* data2 = new GraphDataUnsignedInt(21);

   g->add_node(data1);
   g->add_node(data2);
   g->add_edge(data1, data2, 2.0);

   delete g;
   delete data1;
   delete data2;
}

Iterators

Many methods use lazy iterators as their return value. Here is a small example on handling iterators in C++.

Graph* g = new Graph();
// add nodes and edges to g
// ...
NodePtrIterator *nit = g->get_nodes(); //iterator is allocated on heap
Node *n;
while((n = nit->next()) != NULL) {
   // next() returns NULL when there are no more elements
   // You can do something with node n, but do not add or remove
   // nodes to the graph because this would invalidate the iterator.
}

delete nit; //iterator must be deleted after usage